-
DIFFERENTIAL CALCULUS BY USING NUMERICAL METHODS
The Differential Calculus and the Integrals are constituting the backbone of the mathematical techniques required for the analysis of physical systems. By means of these two mathematical techniques it is possible to describe how specific quantities of interest vary in relation to Space and/or Time.With a given set of data or a function, it may be useful to use Differential Calculus on the data to determine a physical parameter on them that interests us. For example, a particular sequence of data may represent the location of an object as a function of time. In this case, the Derivative and the Second Derivative give the Speed and the Acceleration of the object, respectively.As the derivative is in fact the expression of the gradient of the function, the mathematical expression of it is nothing else but only an expression of the slope. The general idea behind this is that as Δt approaches zero, the Derivative Equation is giving the instantaneous slope of the graph of the function. In numerical terms, this means that if we give to Δt an appropriately small value, the approximation provided must be quite accurate. In order to evaluate and check the error difference resulting from the derivative approach, we use the "Taylor Series".
This ".pdf" File Requires "Chrome 9" or higher, "Firefox 3.6" or higher, "InternetExplorer 9" or higher and the "Adobe PDF Reader" Add-on Installed to Display Properly.
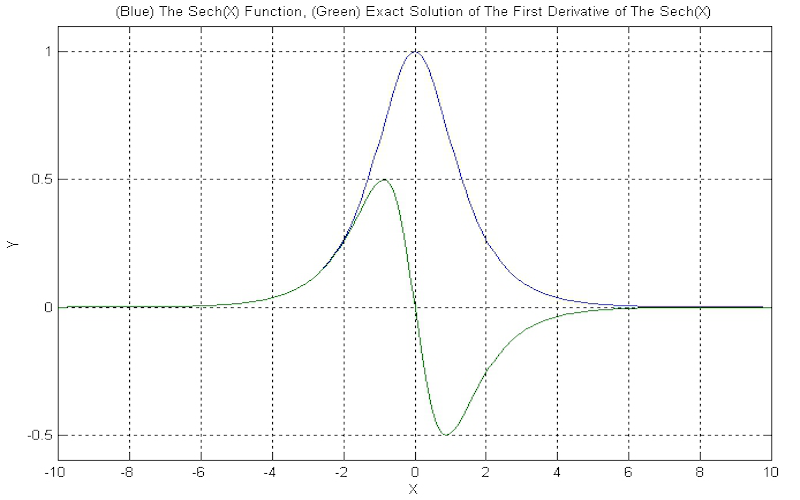
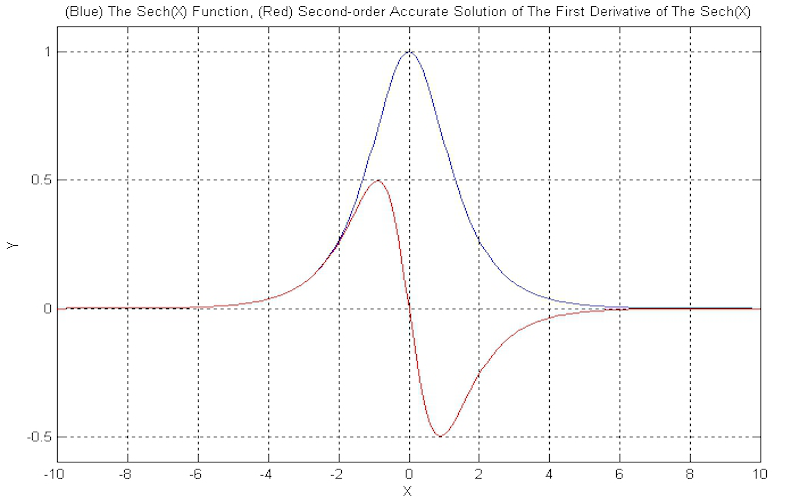
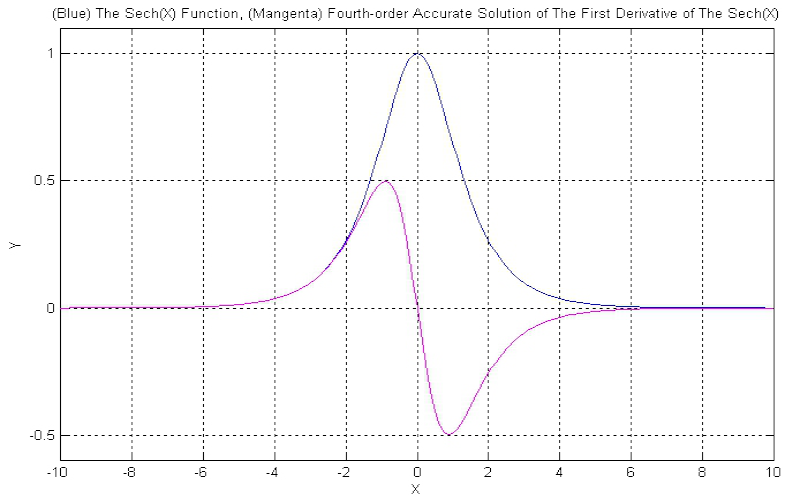
Download "CentreDifferenceMethod"
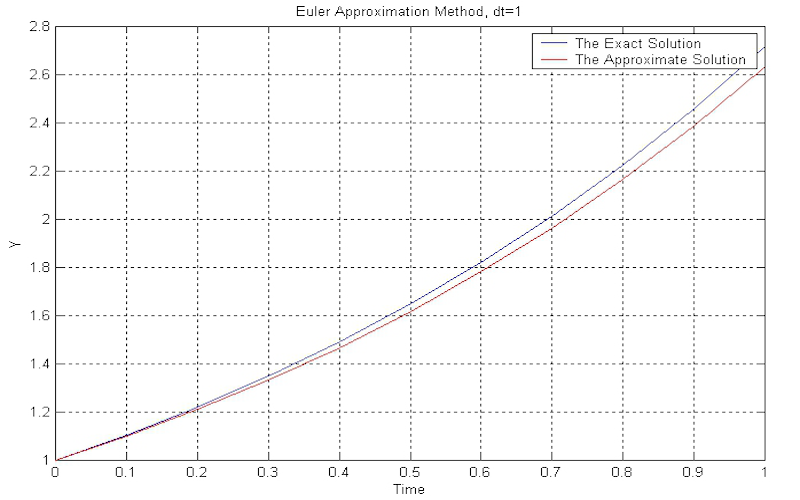
Download "TheEulerMethod"
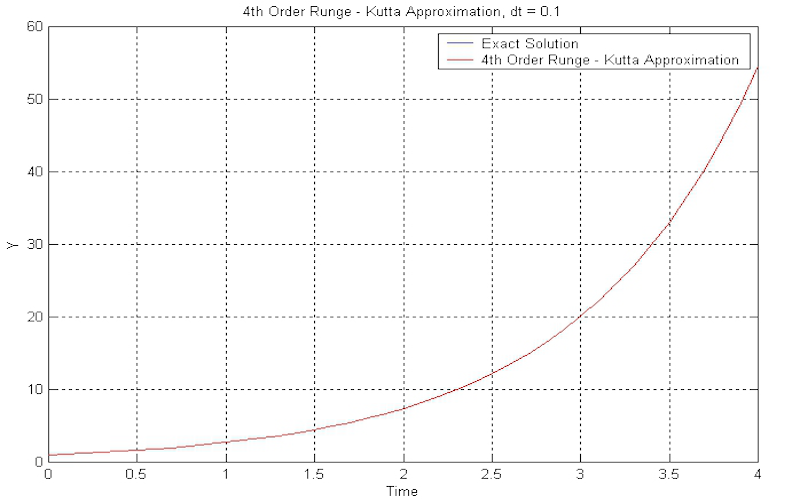
Download "The4thRungeKuttaMethod"
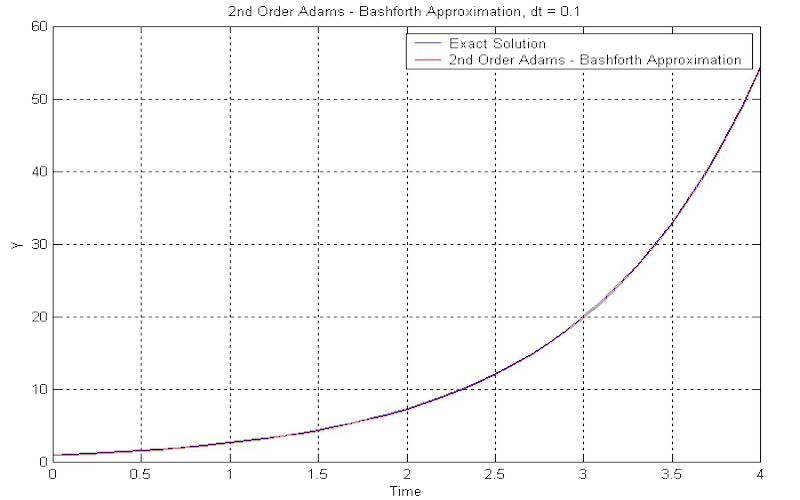
Download "The2ndAdamsBashforthMethod"
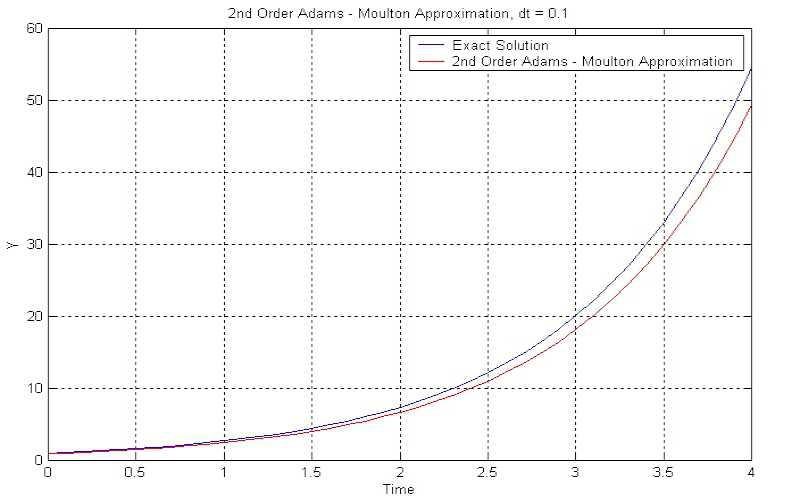
Download "The2ndAdamsMoultonMethod"