-
THE WAVE EQUATION
To become possible to everyone to follow, step by step, the extraction process of the equation describing the motion of Waves and Waveforms, we will base our approach on the ever so popular example of the "Long and Homogeneous Rope". In the case of a long and homogeneous rope with a total Mass ms and Length L the important point that we must turn our attention at is the kind of behaviour exhibited, locally, by each one of its constituent parts (those parts that all put together make up the rope).The expression of the Force of Inertia, needs a restoring Force in a direction equal and opposite (a Force, that is, that works opposite to the Force of Inertia) in order to generate Vibrations. This opposite Force we consider as coming from the Tension T0 exerted on the rope, and more particularly on the two ends of the rope. In the case of our example we use a rope bearing ideal characteristics (like absolute rope elastic properties, etcetera), which has no rigidity to act contrary to its curvature. Let us suppose now that we are taking on the length of the rope (this is axis X on the Cartesian coordinates) a number N of consecutive points.
This ".pdf" File Requires "Chrome 9" or higher, "Firefox 3.6" or higher, "InternetExplorer 9" or higher and the "Adobe PDF Reader" Add-on Installed to Display Properly.
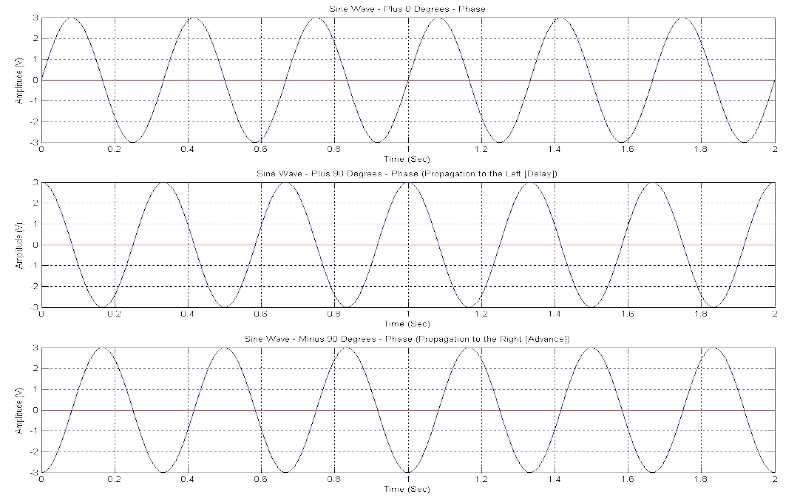
Download "SineWave[90DAdvanceDelay]"
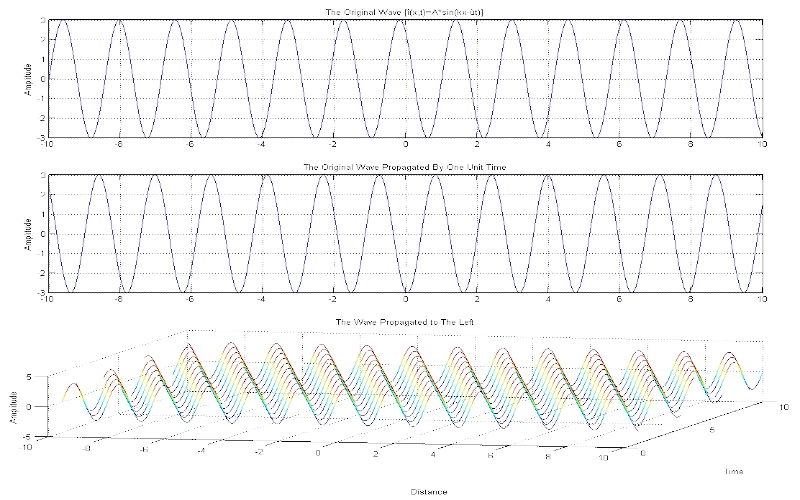
Download "TravellingWavePropagationLeftRight"
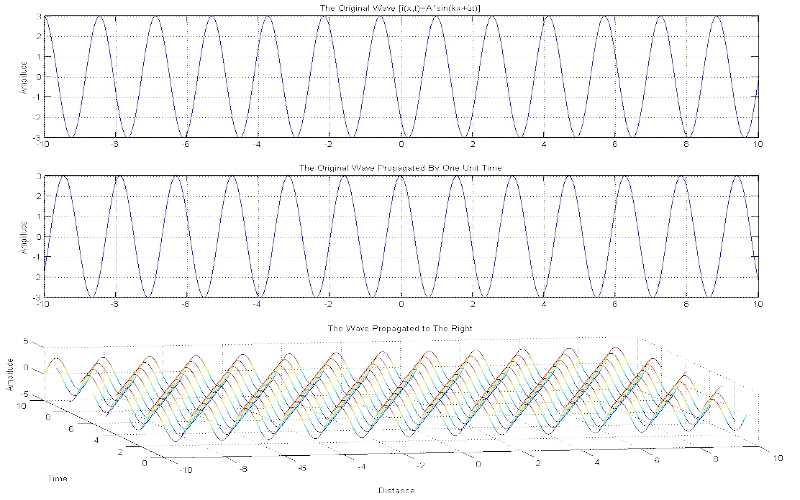
Download "AdvanceDelayNumericalProof"
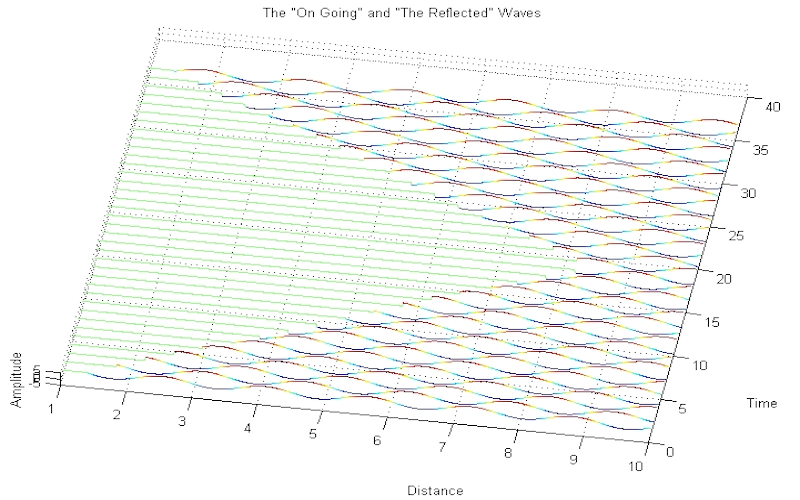
Download "TravellingWaveReflectedFixedEnd"
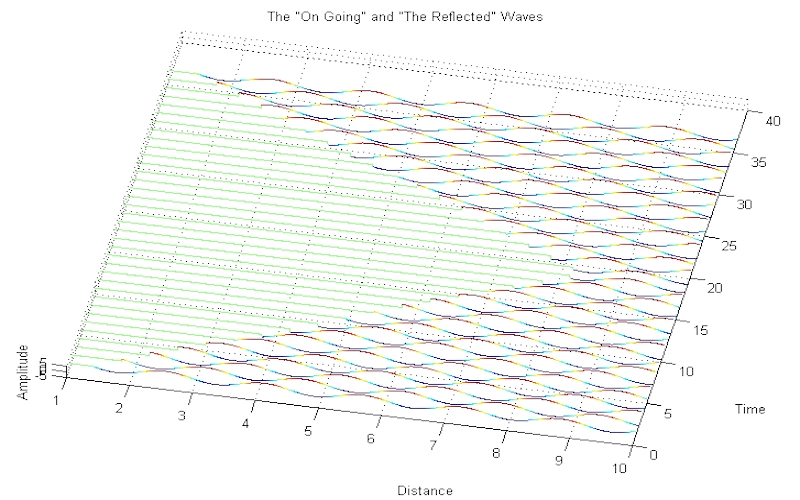
Download "TravellingWaveReflectedFreeEnd"
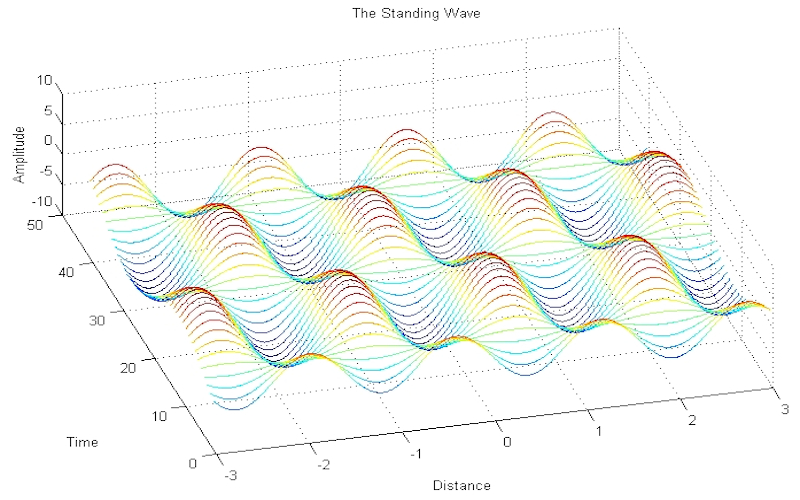
Download "StandingWave"
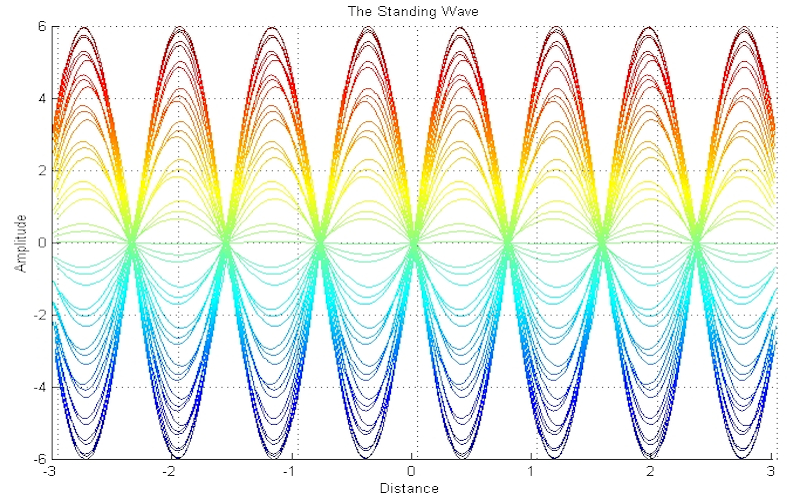
Download "StandingWave"
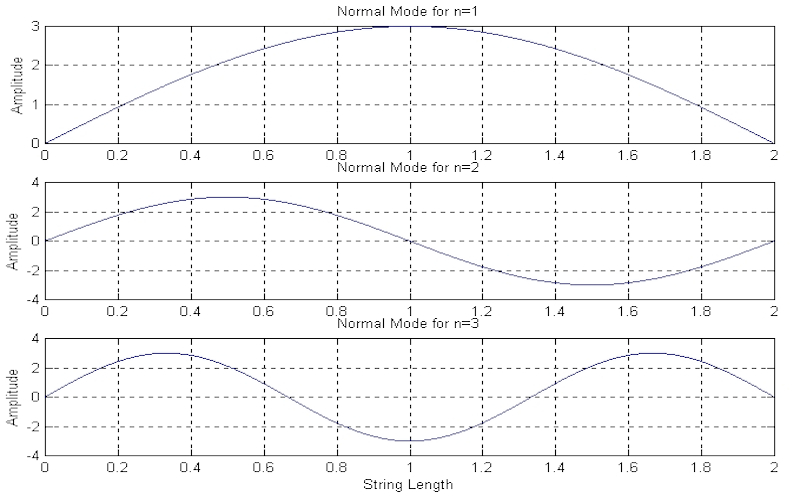
Download "NormalModes"