-
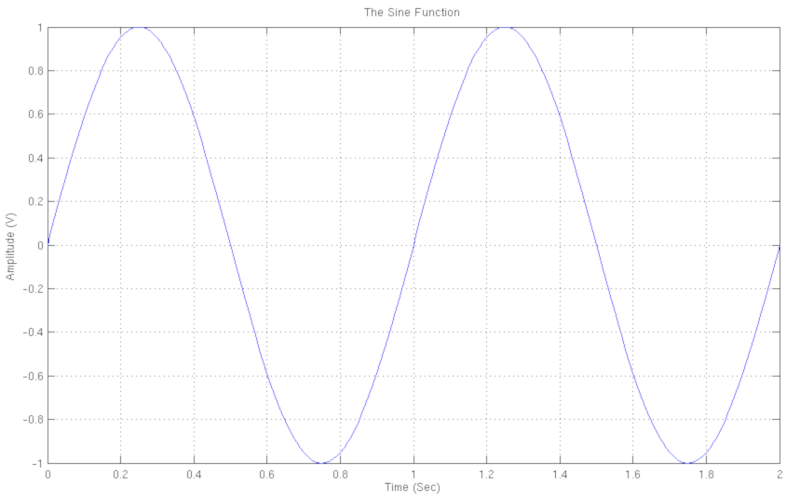
THE SINE FUNCTION
The sine function produces a periodic waveform with specific characteristics. One of the most important is that the first value of the function on the Cartesian Coordinates is zero. For this reason the function mainly finds application in simulations where we generally want the first value to be zero.
Download "SineFunction"
-
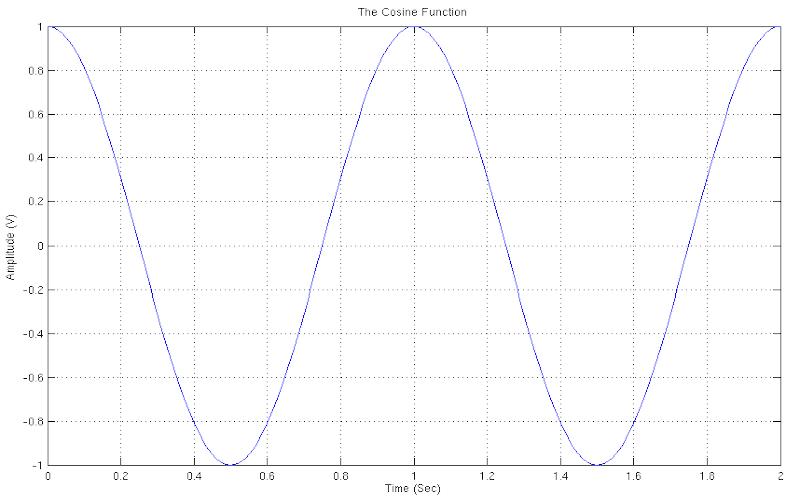
THE COSINE FUNCTION
The Cosine Function produces a periodic waveform with specific characteristics, as well. One of the most important is that the first value of the function on the Cartesian Coordinates is the value one. For this reason, the function finds application mainly in simulations where generally we want the first value taken to be the maximum value (a value of one).
Download "CosineFunction"
-
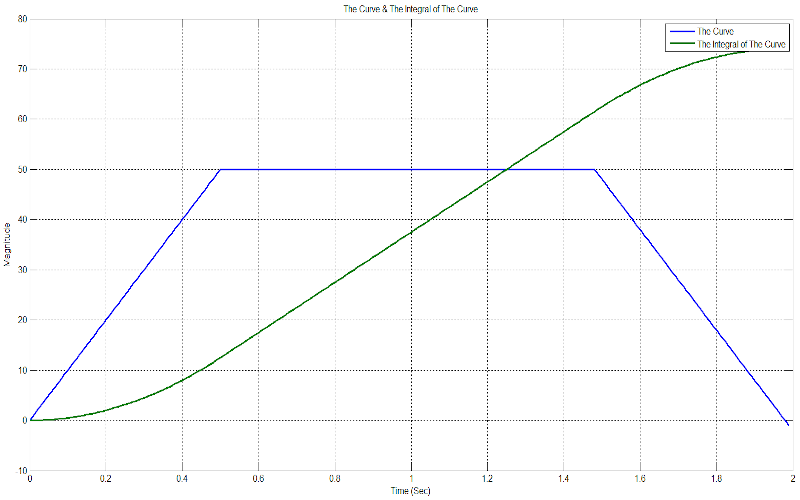
THE LINEARLY INCREASING SINE FUNCTION
This specific form of the Sine function, defers from the original one due to two characteristics. The first characteristic consists the fact that the function does not possess anymore the stable characteristic amplitude value through our its whole range, but its amplitude now increases linearly with time. The second characteristic consists the fact that now the function defines a pure propagation direction from left to right (i.e. from the zero point on the Cartesian Coordinates to plus infinity). The function’s propagation direction vector is defined by its amplitude value, that is, as original starting point of the function is defined or considered the zero amplitude point and the direction of the vector follows its direction of expansion. Thus, any motion on the trajectory of the function experiences two alterations, one from left to right (horizontal displacement), and one from top to bottom (vertical displacement).
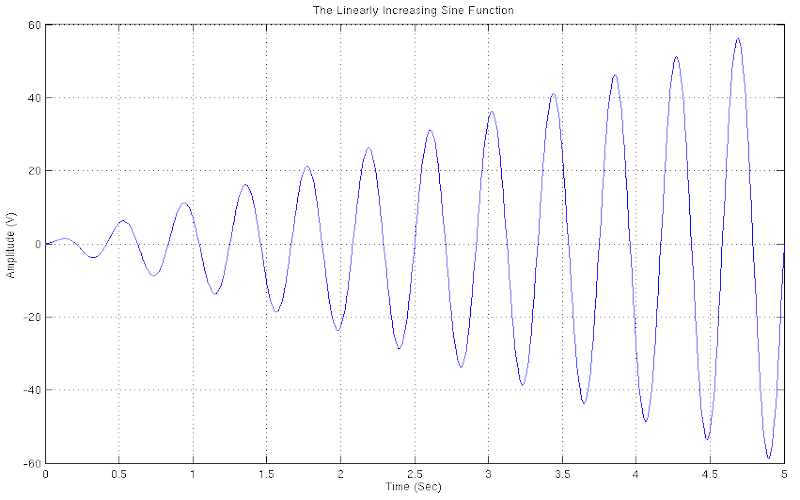
Download "LinearlyIncreasingSineFunction"
-
THE LINEARLY, POSITIVELY ONLY, INCREASING SINE FUNCTION
This form of the sinusoidal function that increases linearly in amplitude, but only in the positive quadrant, is a variation of the original sine function which can be used in a number of important applications. The main difference in relation to the simple ascending form of the function is that it possesses no negative, but only positive values.
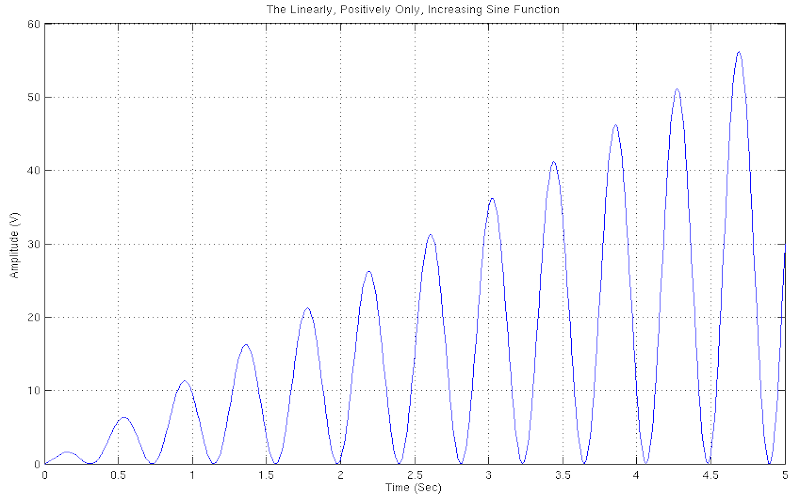
Download "LinearlyIncreasingSineFunctionPositive"
-
THE INCLINED SINE FUNCTION
The inclined sine function is a direct variation of the original sine function, and is obtained by adding only an additional parameter. This parameter characterises and defines how fast the function closes upwards, that is, states indirectly and the angle the function inscribes with the horizontal axis of the Cartesian Coordinates. The parameter, to determine the final form of the function must be multiplied by the current value of the horizontal axis of the Cartesian Coordinates and the result added to the current value of the sine function.
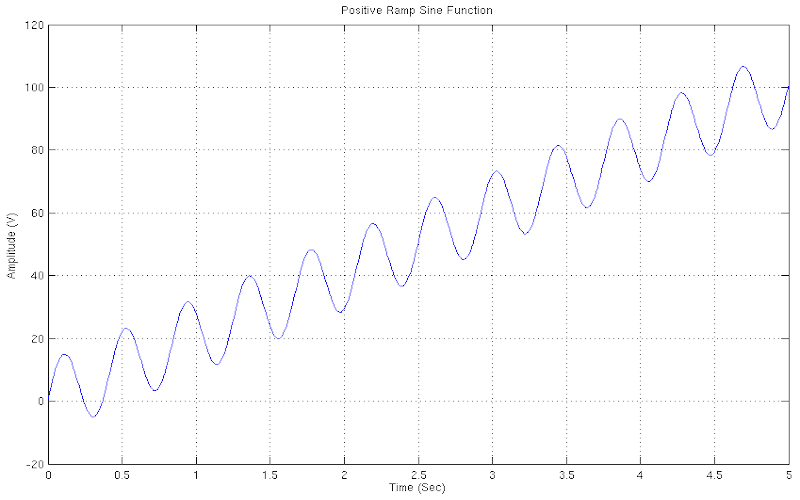
Download "RampIncreasingSineFunction"
-
THE LINEARLY INCREASING IN FREQUENCY SINE FUNCTION
The sine function, as the cosine function as well, under certain conditions, may occur with different frequency values. A variant of the sine function with different frequency values is the linearly increasing in frequency sine function.
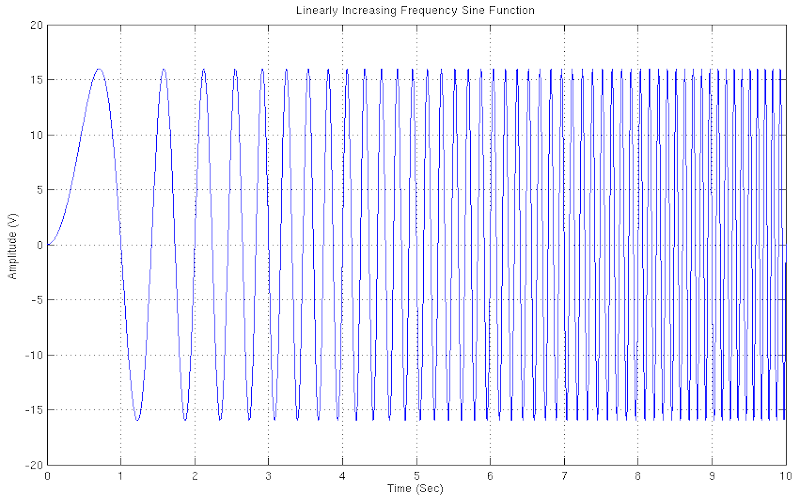
Download "IncreasingFrequencySineFunction"
-
THE MODULATED SINE FUNCTION
In the case that we have two sinusoidal functions multiplied together to give us a third function, we say that we have as a result of the multiplication a modulated sinusoidal function. The configuration of the sinusoidal function comes from the fact that its amplitude value, result of the multiplication, varies in relation to the amplitude of the original sinusoidal function with the lowest frequency. A prerequisite for the creation of a successfully modulated sinusoidal function is one of the two original sinusoidal functions to possess a much higher frequency than the other. Thus the end result we will take will in reality be for the low frequency sinusoidal function to define the amplitude of the high-frequency function. In the science field referred to as: “Digital Signal Processing” (D.S.P.), the modulated sinusoidal function of this type, is referred to as “Amplitude Modulation” (AM).
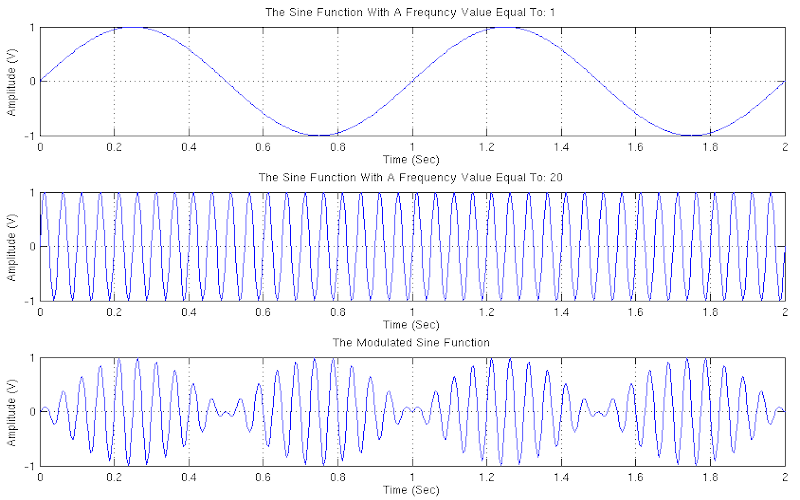
Download "ModulatedSineFunction"
-
THE ASCENDING EXPONENTIAL FUNCTION
Besides the sine and cosine functions, the exponential function is one of those functions that are widely used in the simulation of physical systems. The function comes as a result of rising the constant e (e = 2.71828... ) to the power of the parameter. That is, the function is defined as: e^n with n taking successive values from minus infinity to plus infinity with any step of our choice. This form of the function is the classic form, and sometimes is referred to as: “Ascending Exponential Function”.
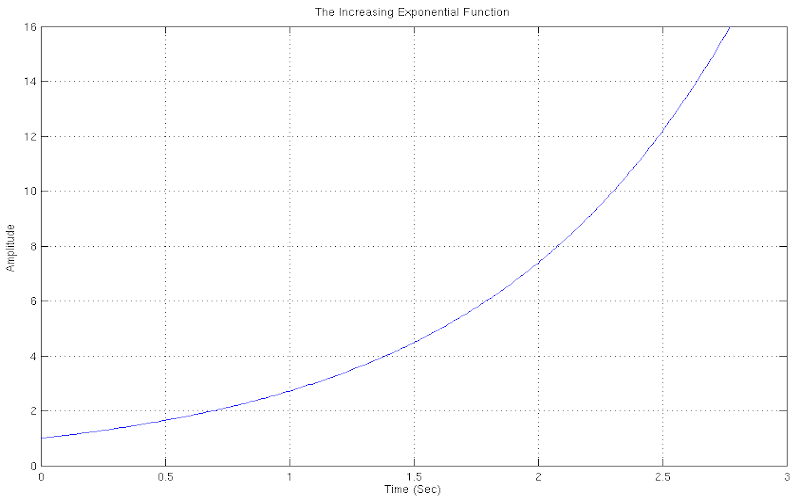
Download "AscendingExponentialFunction"
-
THE DESCENDING EXPONENTIAL FUNCTION
In comparison with the ascending exponential function, the descending exponential function exists as well, whose properties are similar and bear an equal importance for the purpose of simulating physical systems. More specifically, the function finds application in cases where we need to study descending in nature physical systems. Of course, due to the nature of the function itself, the result we take is gradually descending values, which increasingly tend to zero, between the interval [1 ... 0]. The function, unlike all the others we’ve seen so far, possesses two differences but totally equivalent mathematical expressions.
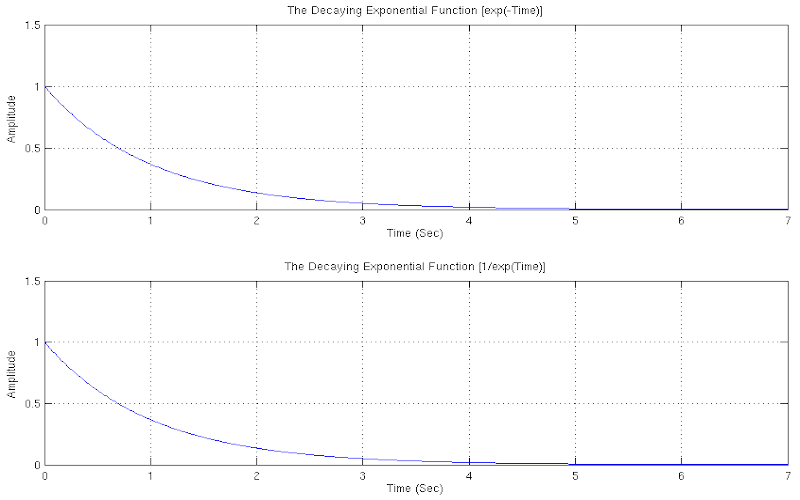
Download "DescendingExponentialFunction"
-
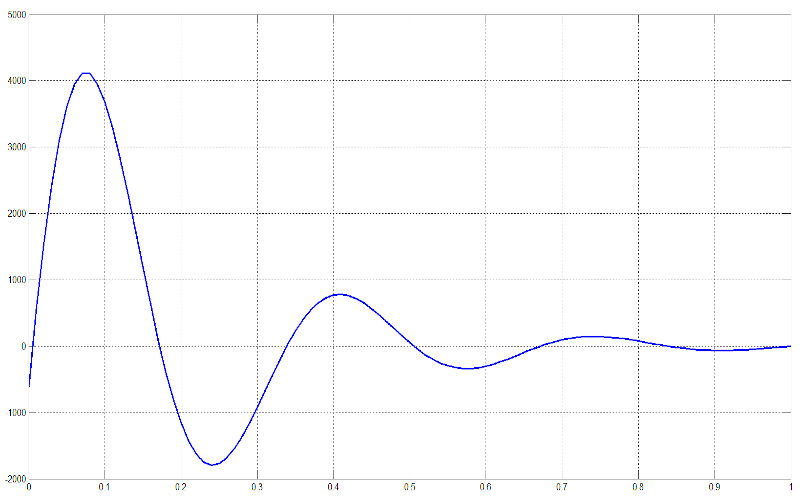
THE COMBINATION OF THE SINE & EXPONENTIAL FUNCTIONS
Despite the fact that the individual study of the functions, as we have seen so far, provides us with an understanding about their properties and how we can use them, is in fact their combination that ultimately gives us the most useful results. So, the first step in further investigating their properties and their practical applications is to have a look at the sort of results will give us the combination of the sine function with the exponential function. The combination of the two functions gives us a third function that is known as: the "Decaying Oscillation” function. A very important feature of the function is the one parameter’s ability to control the decaying speed at which the function is declining towards zero. This parameter, mathematically, is controlled by the value of the variable by which we multiply the value in the exponential function.
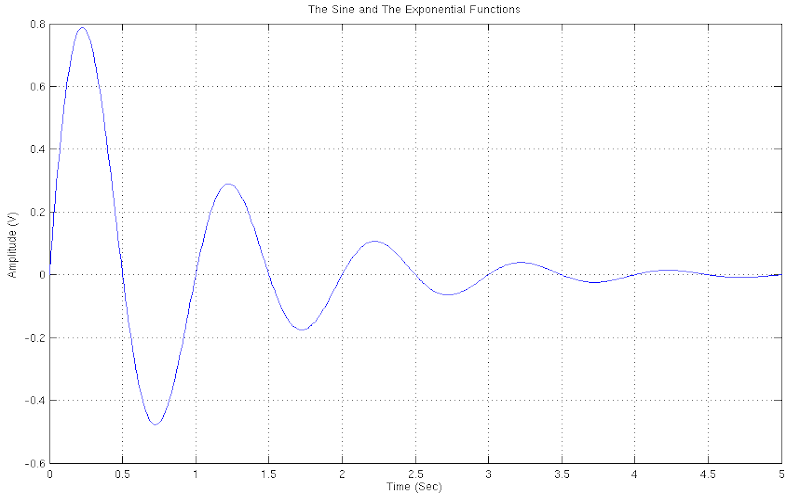
Download "SineAndExponentialFunctions"