C++

EUCLIDEAN ALGORITHM (OR EUCLID’S ALGORITHM)

Computer Programming is nothing more (or less) than another branch of Applied Mathematics, so it is no surprise that the first ever example of an Algorithmic procedure comes from the field of Mathematics. This is the very well known Euclidean Algorithm (or Euclid’s Algorithm). Took its name after the Greek Mathematician Euclid, who for the first time ever in his book “Elements” (300 B.C.) describes an Algorithm that can compute the Greatest Common Divisor (GCD) of two integers (the largest number that divides both integers with a Remainder equal to zero). This example of an Algorithmic step-by-step procedure for performing a calculation according to well-defined rules, is the one Algorithm that started it all!!!

Download "EuclideanAlgorithm"

LINKED LISTS

A “Linked List” is a Linear Collection of Data Elements whose order is not given by their physical placement in Main Memory and each element is pointing to the next one. Consists of a collection of Nodes which collectively represent a Data Sequence. In the most basic form of a Linked List, each Node contains: a) a “Data” section, and b) a “Reference” to the next Node in the sequence. Although Linked Lists can offer an optimum solution to many complex problems, a major drawback is that navigation time through Nodes is Linear with faster access techniques, such as Random Access, not being possible. As a result, Arrays possess better Cache Locality compared to Linked Lists.

This C++ Program materialises the “Single Linked List” approach in how to create Linked Lists, but can very easily extended to any other Linked List approach, along researching new Linked Lists approaches and methodologies. The operational methodology for the Single Linked List implementation is the following:

Initialisation (Stage I): The HEAD & TAIL pointers to Struct are created and set to point to NULL...

First (1st) Node (Stage II): Both HEAD & TAIL pointers are set to point to the same MEMORY LOCATION, that of [Node 1]...

Second (2nd) Node (Stage III): HEAD & TAIL pointers point to different MEMORY LOCATIONS, these of [Node 1] & [Node 2] respectively...

Third (3rd) Node (Stage IV):

For Linked Lists we do not need necessarily to implement both a HEAD and a TAIL Node in the structure!!! If we do so, we end-up having TWO pointers pointing at the very last node in the structure!!! Although it is not necessary, it offers the advantage of locating directly the last Node when we want to add a new one at the end of the List… otherwise, we need to sequentially search for it…!!!

Download "SingleLinkedList"

BINARY SEARCH ALGORITHM

Binary Search (also known as “Half-interval Search”) is a search Algorithm that can best operate to locate a particular element when this element is to be found in a Sorted Array. The operational methodology of the Algorithm focuses on comparing the value of the element in search for with the value of the Middle Element of the Sorted Array. Then, if the two values are not equal, the half-part of the Sorted Array which cannot possibly contain the element we are searching for (because of the Sorted nature of the Array) is eliminated and the search continues on the remaining half-part. The iterations through the Algorithm continue with taking the value of the Middle Element of this part of the Array to compare next with the value of the element we are searching for, and this is repeated until either the element is located or the length of the Array is extinguished, meaning that the element in search was not to be found in the Array in the first place.

Download "BinarySearch"

BINARY SEARCH TREE ALGORITHMS

A Binary Search Tree (also called “Ordered Binary Tree” or “Sorted Binary Tree”), is a Rooted Binary Tree possessing Nodes that each stores a “Key Value” greater than all the key values in its Left Sub-tree and a Key Value less than all the key values in its Right Sub-tree. Binary Trees are usually implemented in order to store data such as numbers in a pre-defined strictly organised way. They allow for all the operational advantages of Binary Search (fast lookup, random insertion & elimination of Nodes, etc.) and they are ideal for developing both Dynamic Sets and Lookup Tables.

The C++ Code provided here is for the “Classic” implementation of the Binary Search Tree Algorithm & two of the nowadays most popular variations on the Classic implementation, the “AVL Binary Search Tree” and the “Red-Black Binary Search Tree”.

The "Classic" Implementation:

The "AVL" Implementation (Original Algorithm):

AVL Binary Search Trees are a kind of self-balancing Binary Search Trees that maintain the difference between heights of Left and Right sub-trees balanced by not allowing their difference to be more than one for all Nodes.

Tree Rotation is an operation that changes the structure of the Tree without interfering with the order of the elements on the AVL Binary Search Tree. The aim is to move one Node “up” in the structure of the Tree and one Node “down”. Thus, it is used to change the shape of the AVL Binary Search Tree, and to decrease its Height by moving Smaller sub-trees “down” and Larger sub-trees “up”, resulting in the improved performance of many classic Tree operations. The Direction of the Rotation depends on the side which the AVL Binary Search Tree Nodes are shifted upon, whilst in other schemes than the traditional one it may Depend on which Child Node takes the Root Node’s place.

Function Descriptions (In The C++ Code):

TreeHeight(AVL *): Calculates the Height of the given AVL Binary Search Tree.

SubTreesHeightDifference(AVL *): Calculates the difference between Height of sub-trees of a given AVL Binary Search Tree.

AVL *RightToRightRotation(AVL *): A Right-To-Right Rotation is a combination of Right Rotation followed by another Right Rotation.

AVL *LeftToLeftRotation(AVL *): A Left-To-Left Rotation is a combination of Left Rotation followed by another Left Rotation.

AVL *Left-To-RightRotation(AVL *): A Left-To-Right Rotation is a combination of Left Rotation followed by another Right Rotation.

AVL *Right-To-LeftRotation(AVL *): A combination of Right Rotation followed by a Left Rotation.

AVL * BalanceTree(AVL *): Performs the Balance operation to the AVL Binary Research Tree by getting the Balance Factor.

AVL * InsertNode(AVL *, int): Performs the Insert Node operation by inserting Nodes in the AVL Binary Search Tree.
DisplayTree(AVL *, int): Displays the Nodes of the AVL Binary Search Tree.
InOrder(AVL *): Traverses an AVL Binary Search Tree in an “In-order” manner.
PreOrder(AVL *): Traverses an AVL Binary Search Tree in a “Pre-order” manner.
PostOrder(AVL *): Traverses an AVL binary Search Tree in a “Post-order” manner.

Download "BinarySearchTreeClassic"

Download "BinarySearchTreeAVL(I)"

The "AVL" Implementation (Variation):

Download "BinarySearchTreeAVL(II)"

The "Red-Black" Implementation (Original):

Download "BinarySearchTreeRedBlack(I)"

The "Red-Black" Implementation (Variation):

Download "BinarySearchTreeRedBlack(II)"

HASH-BASED SEARCH

A Hash-based Searching Algorithm indexes each Array Element with a particular Index Value and then Hash that index value with a mathematical function (most commonly one that involves in one or the other way the “m MOD n” calculation, with “m” being the Index Value & “n” being a user defined number). The major advantage of this type of Algorithms is that they are not dependent on the ordered or unordered nature of the Array since the mapping of the Hash Value with the Index Value is a direct one and that way they manage to achieve a constant performance time.

Download "Hash-basedSearch"

HASH-BASED LINKED LIST SEARCH

Hash-based Linked Lists, especially in Searching related applications, have a better average-case performance than most of the other Algorithms applicable for the same type of applications. The central element in this type of Algorithms is always the Hash-function that is used in order to transform one or more of the characteristics of the searched-for item into a value that can be used as an Index in an Indexed Hash Table. It is exactly this indexed nature of the implementation that permits for such good performance by the Algorithms falling in this category.

Download "Hash-basedLinkedListSearch"

SEQUENTIAL SEARCH

Hash-based Linked Lists, especially in Searching related applications, have a better average-case performance than most of the other Algorithms applicable for the same type of applications. The central element in this type of Algorithms is always the Hash-function that is used in order to transform one or more of the characteristics of the searched-for item into a value that can be used as an Index in an Indexed Hash Table. It is exactly this indexed nature of the implementation that permits for such good performance by the Algorithms falling in this category. The C++ Code provided here covers the “Classic” implementation of the Algorithm & three variations on this classic implementation.

The "Classic" Implementation:

Download "SequentialSearch"

The "Move To Front On Success" (MTFOS) Implementation [Variation]:

Download "SequentialSearchMTFOS"

The "Move Up On Success" (MUOS) Implementation [Variation]:

Download "SequentialSearchMUOS"

The "Move To End On Success" (MTEOS) Implementation [Variation]:

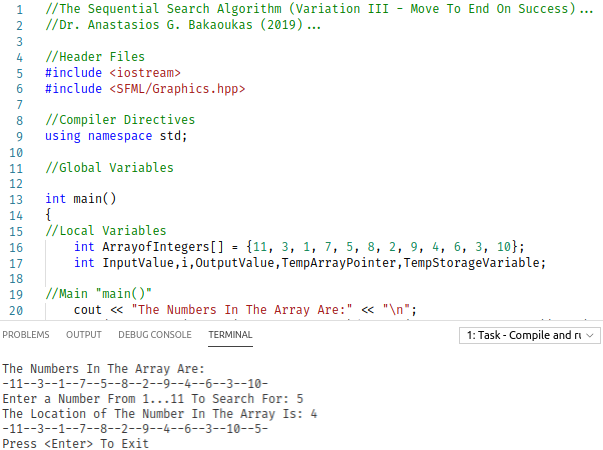
Download "SequentialSearchMTEOS"

BUBBLE SORT ALGORITHM

Bubble Sort is the simplest possible Sorting Algorithm for either Ascending or Descending sorting of a homogeneous set of data. At its core the Algorithm operates in repeating steps throughout the set of elements, comparing in its iteration Adjacent Elements that swaps them around if they are in the wrong order. The Algorithm belongs to a general category of Sorting Algorithms called “Comparison Sort” Algorithms, and has been named “Bubble Sort” because of the way Smaller or Larger Elements in the set supposedly “Bubble” their way to the top of the sorting list. Because of the continues direct comparisons required by the Algorithm (computationally very expensive as operations), performs rather poorly in comparison with other Sorting Algorithms and especially when “Real World” applications are concerned, but still, a valid Sorting Algorithm that achieves the task.

Download "BubbleSort"

ARRAYS IN C++

This program demonstrates the use of Arrays in C++. We can insert new objects in the Array, we can extract objects from an Array, inverse the objects in the Array, isolate the maximum, minimum, and average value of numerical objects in the Array.

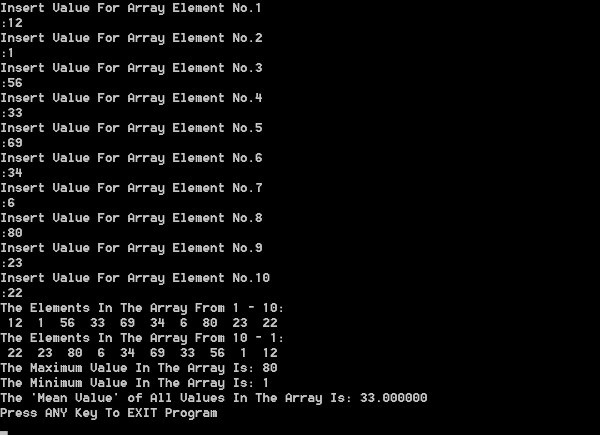
Download "Array"

ASCII ART IN C++ "TRIANGLE" (USING THE "FOR" LOOP)

This program’s focus is on ASCII Art, a very famous and effective way to produce meaningful pictures and logos out of Alphabet characters and punctuation marks. The main programming element in this simple implementation is the “For” loop.

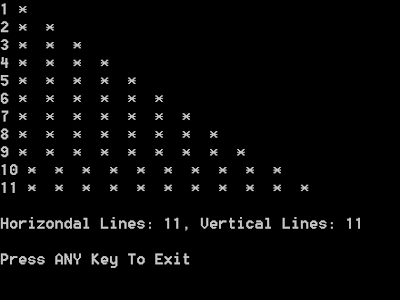
Download "ASCIIArtTriangleWithFor"

C++

Few Words About SCIENZA

Links I

Links II

Terms